L’Etrange volupté de la mathématique littéraire, essai, éd. Jacques Antoine, Bruxelles, 1983, brevet n° 776.587. Cette méthode « montre » les multiples visages de Chéri de Colette et Nombres de Philippe Sollers. Ultérieurement, elle lui a permis plusieurs opportunités d’application notamment sur la Petite Cosmogonie portative de Raymond Queneau (voir section colloques). Adaptation roumaine par Horia Badescu Strania voluptate a matematicii literare, édi. Eminscu, Bucarest, 1998. Invitation au Japon.
Le livre est un objet de l’espace, un parallélépipède. On peut le mesurer. On peut en calculer les proportions. Inscrit dans ce parallélépipède, le texte, objet de la durée, peut-il lui aussi se mesurer ? Peut-on y retrouver les mêmes proportions que l’objet qui le circonscrit ? Entendons : les lois de l’espace et de la durée peuvent-elles coïncider ? Expérimentation sur Chéri de Colette et Nombre de Philippe Sollers.
Illustrations issues de Nombres de Philippe Sollers :
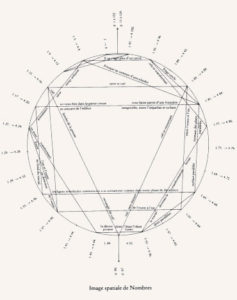
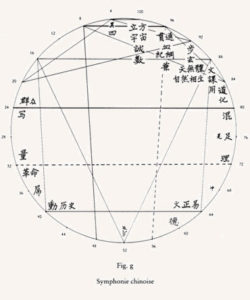

Extrait
Matila Ghyka analyse les proportions et les rythmes dans les arts de l’espace et de la durée (architecture, peinture, musique, poésie, prose). Or, la durée montre un enchaînement de proportions semblables à celles que la « symétria » procure dans les arts de l’espace. Forts de cette constatation, pourquoi Matila Ghyka, et même Paul Valéry, ce « passionné » de la forme, n’ont-ils pas compris que le livre est objet à la fois d’espace et de durée ? Ceux-ci mutuellement mesurables ? Parallélépipède et prosodique intimement liés ?